DiffusionPDE: Generative PDE-Solving
Under Partial Observation

NeurIPS 2024
ICML 2024 AI for Science Workshop (Oral)

Jiahe Huang1  Guandao Yang2  Zichen Wang1  Jeong Joon Park1 

1University of Michigan 
2Stanford University 

Paper Code BibTex Back

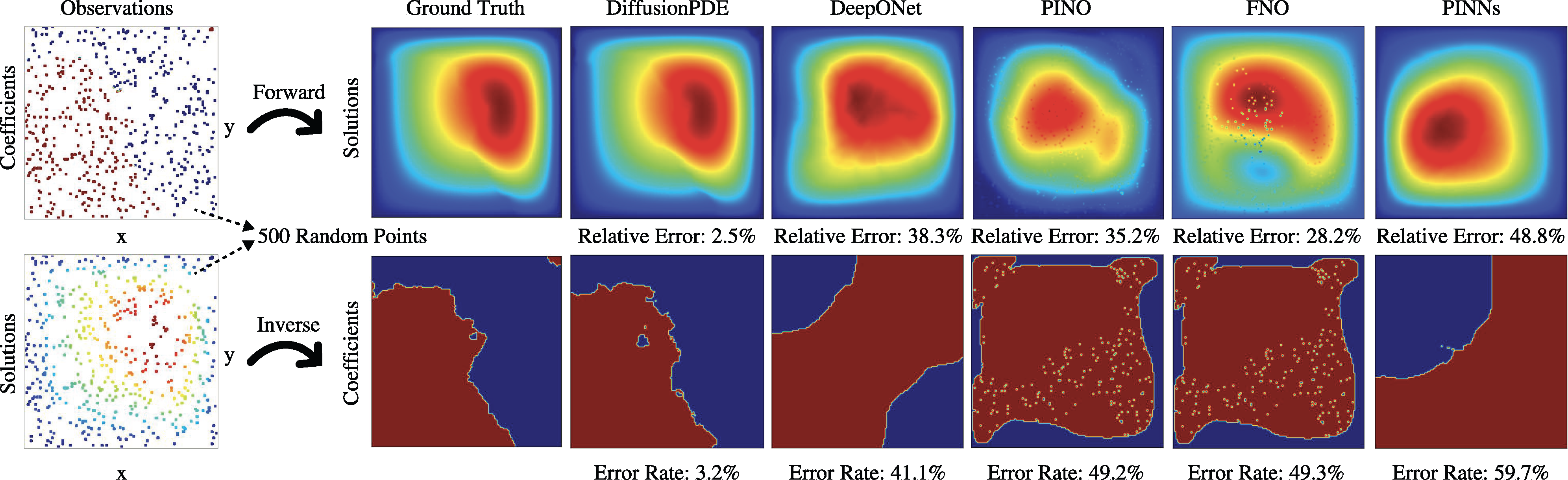
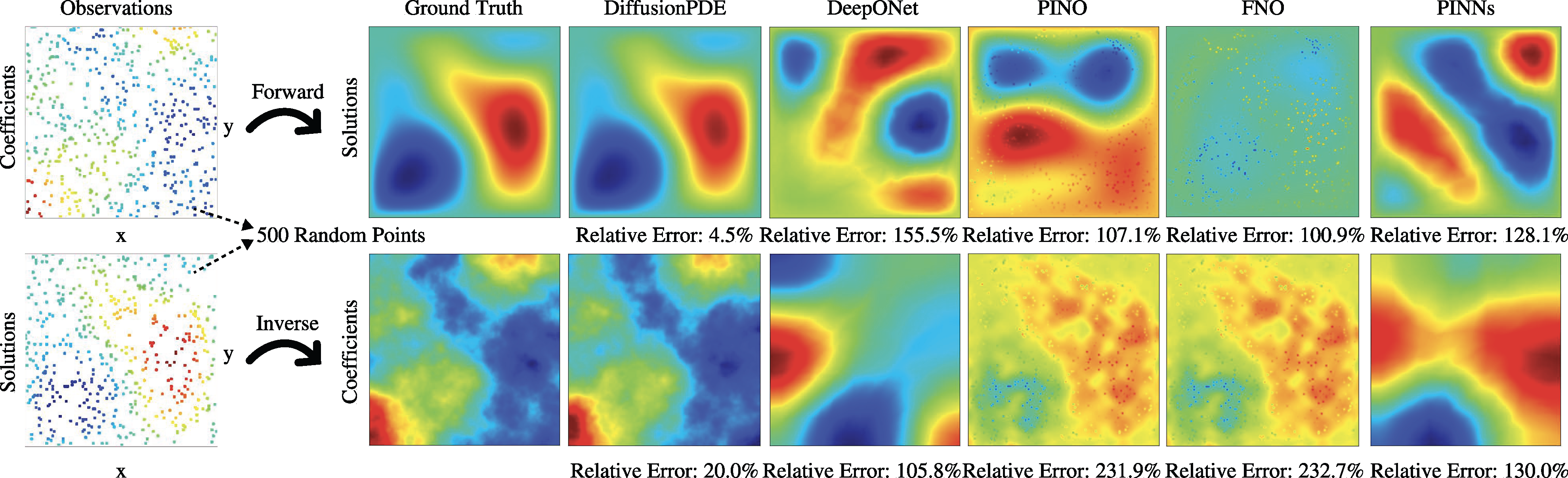
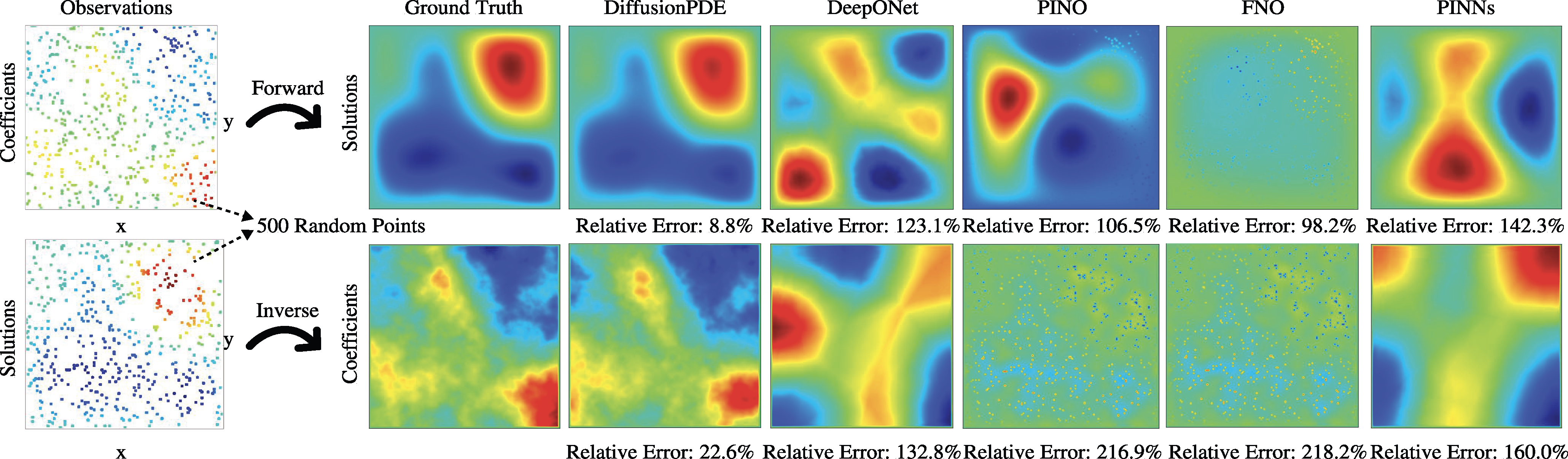
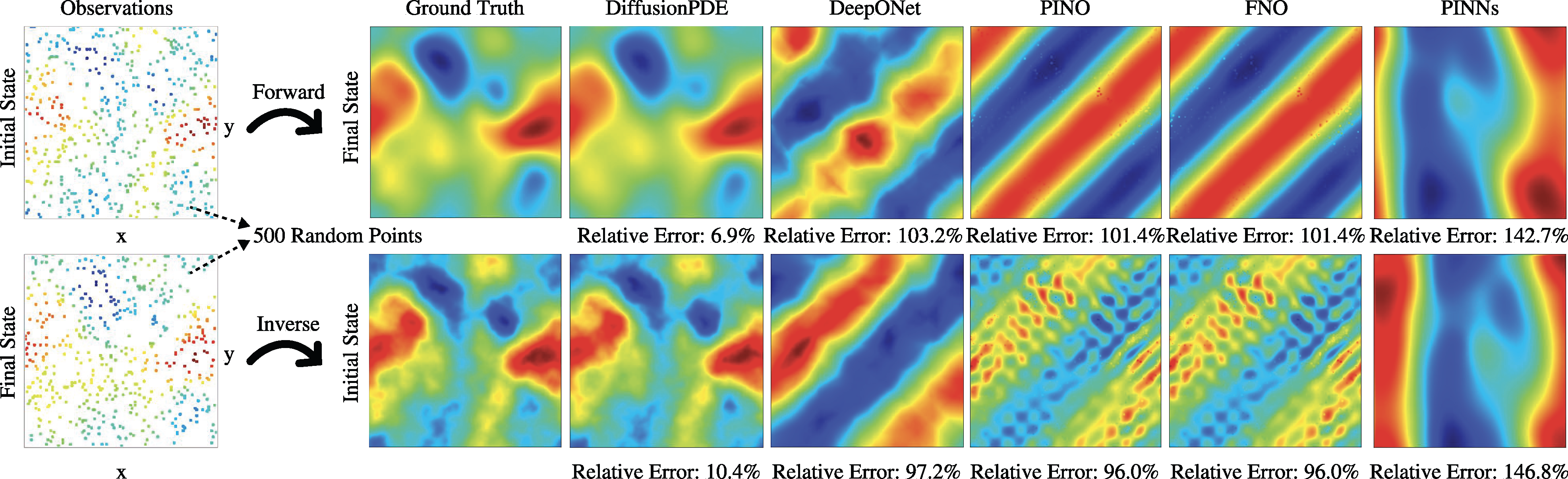
Solving Forward and Inverse Problems: More Results

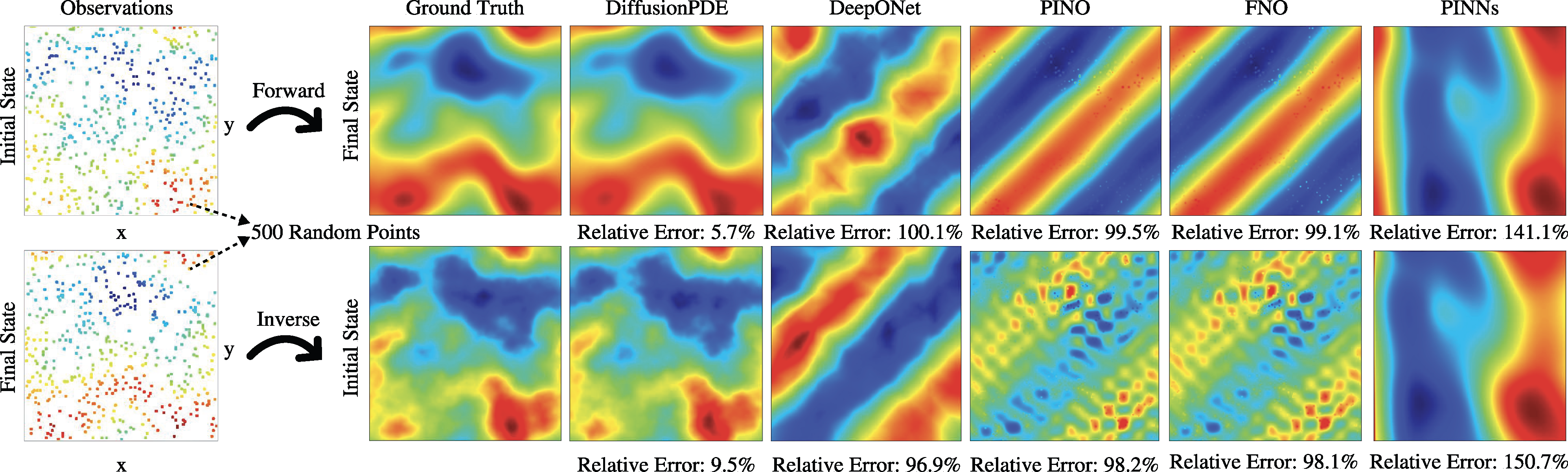
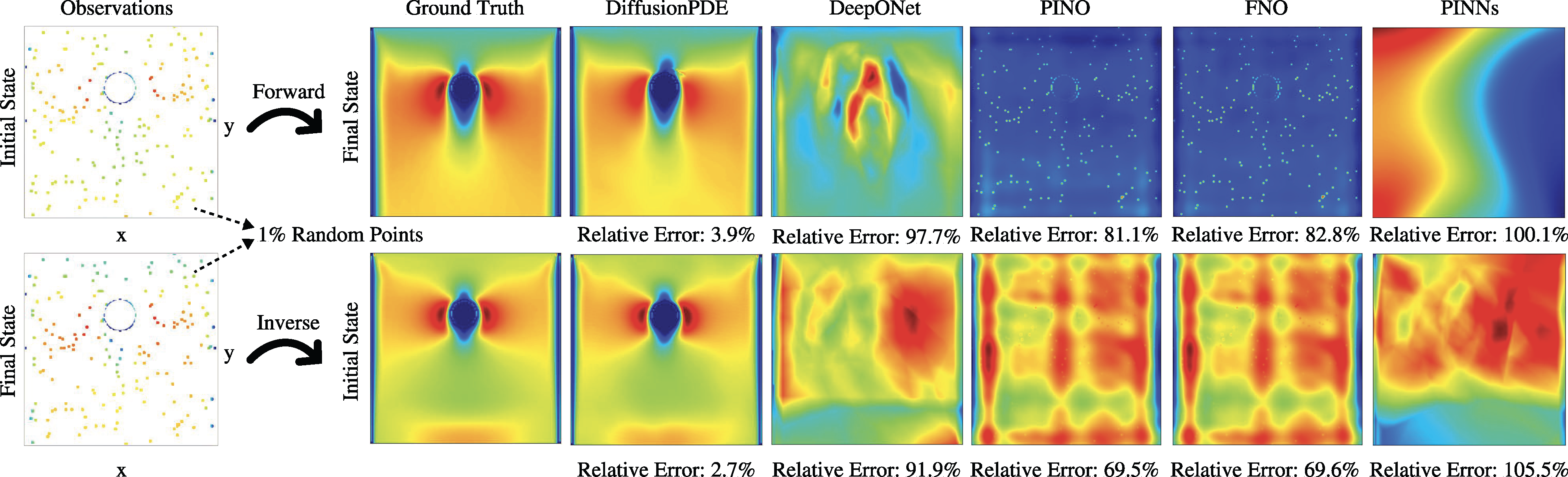
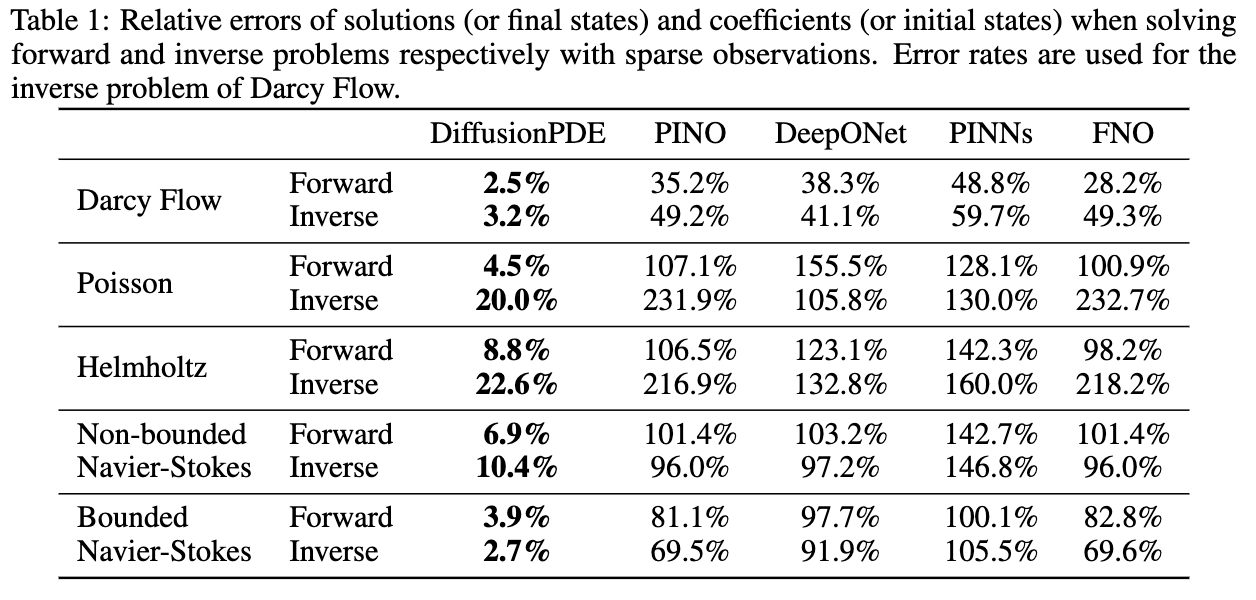
We address both forward and inverse problems of various types of PDEs with partial observations and compare the efficacy of our approach with state-of-the-art methods including DeepONet (Lu et al., 2021), PINO (Li et al., 2021), FNO (Li et al., 2020), and PINNs (Raissi et al., 2019). We show the relative errors of all methods regarding both forward and inverse problems with 500 observation points in Table 1. Since the coefficients of Darcy Flow are binary, we evaluate the error rates of our prediction. Non-binary data is evaluated using mean pixel-wise relative error. We report error numbers averaged across 1,000 random scenes and observations for each PDE. DiffusionPDE outperforms all other methods.

More examples of the forward and inverse problems are shown below.

Bounded Darcy Flow with 500 observation points of the coefficient or the solution.
Bounded Poisson Equation with 500 observation points of the coefficient or the solution.
Bounded Helmholtz Equation with 500 observation points of the coefficient or the solution.
Two samples of non-bounded Navier-Stokes Equation for vorticity with 500 observation points of the initial state or the final state.
Bounded Navier-Stokes Equation for velocity with a random circular obstacle and 1% observation points at the initial state or the final state.
Back

BibTeX


@misc{huang2024diffusionpdegenerativepdesolvingpartial,
    title={DiffusionPDE: Generative PDE-Solving Under Partial Observation}, 
    author={Jiahe Huang and Guandao Yang and Zichen Wang and Jeong Joon Park},
    year={2024},
    eprint={2406.17763},
    archivePrefix={arXiv},
    primaryClass={cs.LG}
    url={https://arxiv.org/abs/2406.17763}, 
}